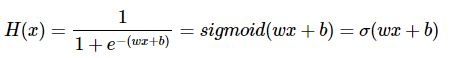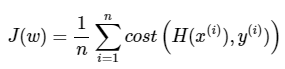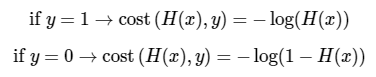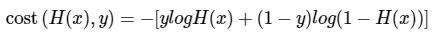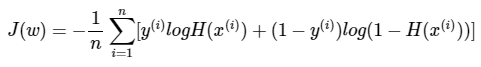뒤로가기

MachineLearning

머신 러닝 로지스틱 회귀

이현우 2022.12.01.

시험을 봤는데 이 점수가 합격인지 불합격인지, 메일을 받았을 때 이 메일이 정상 메일인지 스팸 메일인지를 예상하는 문제들이 있을 수 있습니다.

이렇게 두 개의 선택지 중에서 하나를 결정하는 문제를 이진 분류(Binary Classification)라고 합니다.

그리고 이런 문제를 풀기 위한 대표적인 알고리즘으로 로지스틱 회귀(Logistic Regression)가 있습니다.

비용 함수, 가설 등의 개념은 앞의 머신 러닝 선형 회귀 포스트를 참고하시기 바랍니다.

1. 이진 분류(Binary Classification)

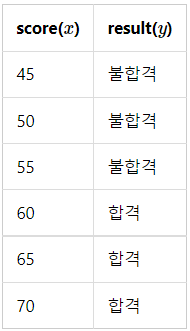
시험 성적에 따라서 합격, 불합격이 기재된 데이터가 있다고 하고, 시험 성적을 x, 합불 결과를 y라고 하겠습니다.

이 데이터로부터 특정 점수를 얻었을 때의 합격, 불합격 여부를 판정하는 모델을 만들고자 합니다.

/images/2022-12-01-MachineLearning-LogisticRegression/binaryclassification1.PNG

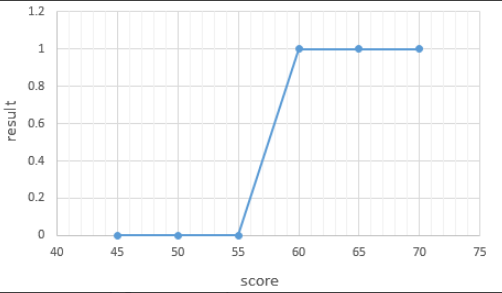
합격을 1, 불합격을 0이라고 하였을 때 그래프를 그려보면 다음과 같습니다.

/images/2022-12-01-MachineLearning-LogisticRegression/binaryclassification2.PNG

그래프는 S자 형태로 표현됩니다. 이러한 x와 y의 관계를 표현하기 위해서는 직선을 표현하는 함수가 아니라 S자 형태로 표현할 수 있는 함수가 필요합니다.

출력이 0과 1사이의 값을 가지면서 S자 형태로 그려지는 함수로 시그모이드 함수(Sigmoid function)가 있습니다.

2. 시그모이드 함수(Sigmoid function)

시그모이드 함수는 종종 σ(소문자 시그마)로 축약해서 표현하기도 합니다.

로지스틱 회귀를 풀기 위한 가설을 세워봅니다. (e는 자연 상수 2.718281…)

/images/2022-12-01-MachineLearning-LogisticRegression/sigmoid1.PNG

여기서 구해야 할 것은 주어진 데이터에 가장 적합한 가중치 w(weight)와 편향 b(bias)입니다.

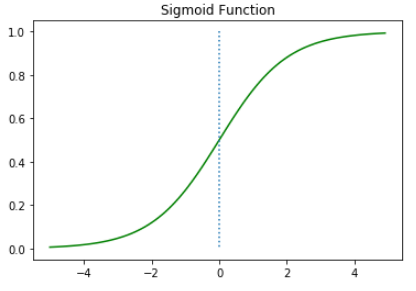
시그모이드 함수를 그래프로 시각화 해보면 다음과 같습니다.

import numpy as np
import matplotlib.pyplot as plt
 
def sigmoid(x):
    return 1/(1+np.exp(-x))
 
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
 
plt.plot(x, y, 'g')
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()

/images/2022-12-01-MachineLearning-LogisticRegression/sigmoid2.PNG

위의 그래프처럼 시그모이드 함수는 출력값을 0과 1사이의 값으로 조정하여 반환합니다.

가중치 w와 편향 b이 출력값에 어떤 영향을 미치는지 시각화를 통해 알아보겠습니다.

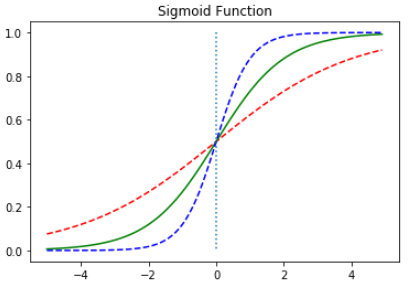
우선 가중치 w에 따른 그래프의 변화를 보겠습니다.

import numpy as np
import matplotlib.pyplot as plt
 
def sigmoid(x):
    return 1/(1+np.exp(-x))
 
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(0.5*x)
y2 = sigmoid(x)
y3 = sigmoid(2*x)
 
plt.plot(x, y1, 'r', linestyle='--') # w의 값이 0.5일때
plt.plot(x, y2, 'g') # w의 값이 1일때
plt.plot(x, y3, 'b', linestyle='--') # w의 값이 2일때
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()

/images/2022-12-01-MachineLearning-LogisticRegression/sigmoid3.PNG

빨간선은 w의 값이 0.5, 초록선은 w의 값이 1, 파란선은 w의 값이 2인 경우입니다. w의 값이 커지면 경사가 커지고 w의 값이 작아지면 경사가 작아집니다.

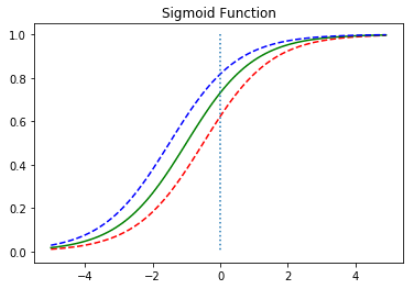
다음은 편향 b값에 따라서 그래프가 이동하는 것을 보여줍니다.

import numpy as np
import matplotlib.pyplot as plt
 
def sigmoid(x):
    return 1/(1+np.exp(-x))
 
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(x+0.5)
y2 = sigmoid(x+1)
y3 = sigmoid(x+1.5)
 
plt.plot(x, y1, 'r', linestyle='--') # x + 0.5
plt.plot(x, y2, 'g') # x + 1
plt.plot(x, y3, 'b', linestyle='--') # x + 1.5
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()

/images/2022-12-01-MachineLearning-LogisticRegression/sigmoid4.PNG

이러한 시그모이드 함수는 0부터 1까지의 값을 가지는데 출력값이 0.5 이상이면 1(True), 0.5 이하면 0(False)로 만들면 이진 분류 문제를 풀기 위해 사용할 수 있습니다.

3. 비용 함수(Cost function) : 크로스 엔트로피 함수(Corss Entropy Function)

로지스틱 회귀 또한 경사 하강법을 사용하여 가중치 w를 찾아내지만, 비용 함수로는 평균 제곱 오차를 사용하지 않습니다.

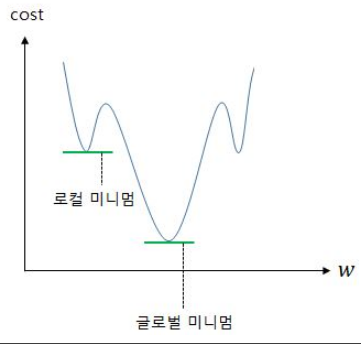
평균 제곱 오차를 로지스틱 회귀의 비용 함수로 사용했을 때는 로컬 미니멈에 빠질 가능성이 지나치게 높아 문제 해결이 어렵습니다.

/images/2022-12-01-MachineLearning-LogisticRegression/cost1.PNG

  • 글로벌 미니멈(Global Minimum) : 전체 함수에 걸쳐 최소값
  • 로컬 미니멈(Local Minimum) : 글로벌 미니멈이 아닌 특정 구역에서의 최소값

로지스틱 회귀에서 평균 제곱 오차를 비용 함수로 사용하면, 경사 하강법을 사용하였을 때 로컬 미니멈에 빠질 가능성이 매우 높습니다.

실제값과 예측값의 오차를 나타내며 실제 값과 예측 값에 대한 오차를 줄이는 비용 함수(cost function)를 쓰면 다음과 같습니다.

/images/2022-12-01-MachineLearning-LogisticRegression/cost2.PNG

시그모이드 함수는 0과 1사이의 y값을 반환합니다.

이는 실제 값이 0일 때 y값이 1에 가까워지면 오차가 커지며, 실제 값이 1일 때 y값이 0에 가까워지면 오차가 커짐을 의미합니다.

이를 반영할 수 있는 함수는 로그 함수를 통해 표현 가능합니다.

/images/2022-12-01-MachineLearning-LogisticRegression/cost3.PNG

y의 실제 값이 1일 때 -logH(x) 그래프를 사용하고 y의 실제 값이 0일 때 -log(1 - H(x)) 그래프를 사용해야 합니다.

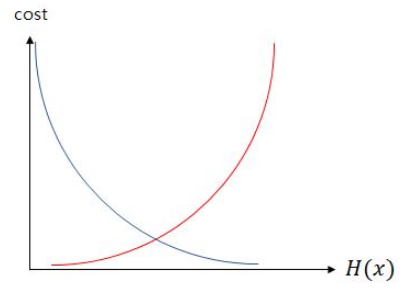
/images/2022-12-01-MachineLearning-LogisticRegression/cost4.PNG

파란색 선은 실제 값 y가 1일 때의 -log(H(x))의 그래프를 빨간색 선은 실제 값 y가 0일 때의 -log(1 - H(x))의 그래프를 나타냅니다.

그래프를 보면 실제 값이 1일 때, 예측 값인 H(x)의 값이 1이면 오차가 0이므로 당연히 cost는 0이 됩니다.

반면, 실제 값이 1일 때, H(x)의 값이 0으로 수렴하면 cost는 무한대로 발산합니다.

실제 값이 0인 경우는 그 반대로 이해하면 됩니다.

이는 다음과 같이 하나의 식으로 표현할 수 있습니다.

/images/2022-12-01-MachineLearning-LogisticRegression/cost5.PNG

y와 (1-y)가 식 중간에 들어갔고, 두 개의 식을 -로 묶은 것 외에는 기존의 두 식이 들어가 있는 것을 볼 수 있습니다.

y가 0이면 ylogH(x)가 없어지고, y가 1이면 (1-y)log(1-H(x))가 없어지는데 이는 각각 y가 1일 때와 y가 0일 때의 앞서 본 식과 동일합니다.

결과적으로 로지스틱 회귀의 목적 함수는 다음과 같습니다.

/images/2022-12-01-MachineLearning-LogisticRegression/cost6.PNG

로지스틱 회귀에서 찾아낸 비용 함수를 크로스 엔트로피(Cross Entropy)함수라고 합니다.

결론적으로 로지스틱 회귀는 비용 함수로 크로스 엔트로피 함수를 사용하며, 가중치를 찾기 위해서 크로스 엔트로피 함수의 평균을 취한 함수를 사용합니다.

크로스 엔트로피 함수는 소프트맥스 회귀(다중 분류에서 사용)의 비용 함수이기도 합니다.

4. 코드를 이용한 간단한 실습

독립 변수 데이터를 x, 숫자 10 이상인 경우에는 1, 미만인 경우에는 0을 부여한 레이블 데이터를 y라고 하겠습니다.

x = [-50, -40 ,-30, -20, -10, -5, 0, 5, 10, 20, 30, 40, 50]

y = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]

4.1 케라스(Keras)를 이용한 실습

데이터는 1개의 실수 x로부터 1개의 실수인 y를 예측하는 맵핑관계를 가지므로

  • Dense의 output_dim, input_dim 인자값으로 각각 1을 기재합니다.
  • 시그모이드 함수를 사용할 것이므로 activation의 인자값으로는 sigmoid를 기재해줍니다.
  • 옵티마이저로는 가장 기본적인 경사 하강법인 sgd를 사용하였습니다.
  • 시그모이드 함수를 사용한 이진 분류 문제에 손실 함수로 크로스 엔트로피 함수를 사용할 경우 binary_crossentropy를 기재해주면 됩니다.
  • 에포크는 200으로 합니다.
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
 
x = np.array([-50, -40, -30, -20, -10, -5, 0, 5, 10, 20, 30, 40, 50])
y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]) # 숫자 10부터 1
 
model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))
 
sgd = optimizers.SGD(lr=0.01)
model.compile(optimizer=sgd, loss='binary_crossentropy', metrics=['binary_accuracy'])
 
model.fit(x, y, epochs=200)

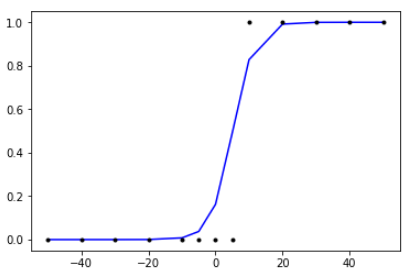
실제 값과 오차를 최소화하도록 값이 변경 된 w와 b의 값을 가진 모델을 이용하여 그래프를 그려보겠습니다.

plt.plot(x, model.predict(x), 'b', x,y, 'k.')
plt.show()

/images/2022-12-01-MachineLearning-LogisticRegression/keras.PNG

x의 값이 5와 10 사이의 어떤 값일 때 y값이 0.5가 넘기 시작하는 것처럼 보입니다.

적어도 x의 값이 5일 때는 y값이 0.5보다 작고, x의 값이 10일 때는 y값이 0.5를 넘을 것입니다.

이제 x의 값이 5보다 작은 값일 때와 x의 값이 10보다 클 때에 대해서 y값을 출력해보겠습니다.

print(model.predict([1, 2, 3, 4, 4.5]))
print(model.predict([11, 21, 31, 41, 500]))

아래의 결과로 x의 값이 5보다 작을 때는 0.5보다 작은 값을, x의 값이 10보다 클 때는 0.5보다 큰 값을 출력하는 것을 볼 수 있습니다.

[[0.21071826]
 [0.26909265]
 [0.33673897]
 [0.41180944]
 [0.45120454]]
[[0.86910886]
 [0.99398106]
 [0.99975663]
 [0.9999902 ]
 [1.        ]]

4.2 싸이킷런(Scikit-Learn)을 이용한 실습

from sklearn.linear_model import LogisticRegression
 
x = np.array([[-50], [-40], [-30], [-20], [-10], [-5], [0], [5], [10], [20], [30], [40], [50]])
y = np.array([[0], [0], [0], [0], [0], [0], [0], [0], [1], [1], [1], [1], [1]])
 
model = LogisticRegression()
model.fit(x, y)

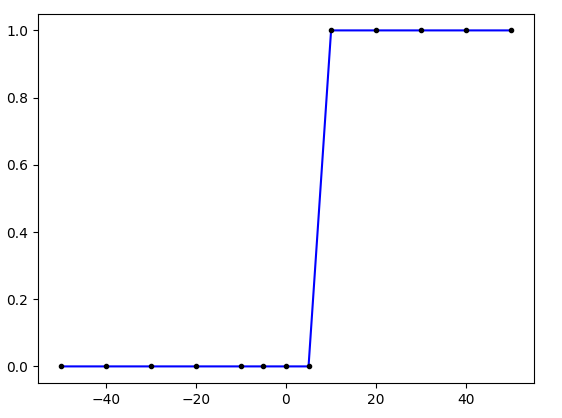
실제 값과 오차를 최소화하도록 값이 변경 된 w와 b의 값을 가진 모델을 이용하여 그래프를 그려보겠습니다.

plt.plot(x, model.predict(x), 'b', x,y, 'k.')
plt.show()

/images/2022-12-01-MachineLearning-LogisticRegression/scikitlearn.PNG

참고 문서

  • 텐서플로우로 시작하는 딥러닝 기초(부스트코스 무료 강의) - https://www.boostcourse.org/ai212/joinLectures/25072
  • 딥 러닝을 이용한 자연어 처리 입문(위키독스) - https://wikidocs.net/22881
  • 혼자 공부하는 머신러닝+딥러닝(서적)